A usual problem which arises in many image processing applications is the corruption of images by different kinds of noise, which leads to the degradation of their perceived quality. To deal with this problem, researchers in the field of image processing and analysis, have developed, over the years, various filtering algorithms for noise removal. The purpose of this Web Page is to present three adaptive nonlinear order statistics filters for noise removal, namely the:
The adaptive LMS L filter's output is defined by the linear combination of the order statistics of the input samples in the filter window:
![]()
The coefficient vector a(k) is adapted at each step k accordingly to the LMS adaptation algorithm.
The adaptive LMS Ll filter is an extension of the adaptive LMS L filter in that it preserves both space or time and order information. This is achieved by proper modification of the ordered input vector. Its output is calculated by use of the equation:
![]()
For the adaptation of its coefficient vector c(k), the LMS algorithm is considered here as well.
The modified SAM filters adapt their behaviour in accordance with the local signal to noise ratio. Thus, they behave differently in homogeneous regions or edge regions. Their output is given by:
![]()
The difference between the symmetrical and the morphological SAM filters lies
only in the local window adaptation method, that they employ. The former adapts the window
size in a symmetrical way, while the latter performs assymetrical window
increment/decrement.
For the comparison of the performance of the proposed filters, a reference image called: Airfield, has been corrupted by the contaminated gaussian noise model:
![]()
The performance results in respect with SNR, PSNR, MAE and MSE measured on the processed versions of a noisy image (Airm0s9l02), by the adaptive L, by the adaptive Ll, by the symmetrical SAM and by the morphological SAM filters, are concentrated in the following table:
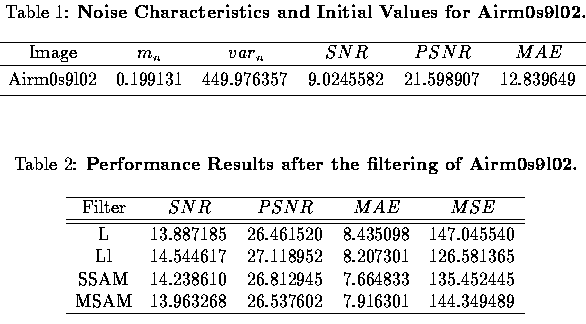
The observation of both performance results and processed images leads to the following conclusions: