
Project Anthivolon attempts to classify systematically, with digital means, cultural treasures from the Byzantine era. For this purpose, a database product has been developed to address the specific needs of artwork conservators and researchers. In this page, certain products of the ongoing research are presented. In the following, some results regarding application of digital image processing and analysis methods will be presented. This page will be updated constantly.
Usually, high resolution acquisition of a large painting is performed indirectly
through the acquisition of smaller, overlapping regions (tiles) of the painting. For this
purpose, a camera is mounted on a positioning unit which is controllable by a computer
system. The following figure represents an example of this acquisition process, where four
tiles were generated.

Image processing methods can be utilized to combine these tiles ("mosaicing")
and produce a high resolution digital representation of the painting. The following figure
displays the result of the mosaicing operation, when applied to the example of the
previous paragraph.

The problem is that optimal mosaicing, that is the process of globally estimating the relative position of each image with respect to each other, is a computation-intensive process, that becomes prohibitive as the search area increases. Methods have been researched which offer significant improvement in speed, while sacrificing little in terms of visual quality. These methods are presented briefly below.
According to the spanning tree procedure, each image is corresponded with a node and each trivial mosaicing with an edge of a graph-grid. The minimum matching error of each edge of graph is evaluated and then the following steps are followed for each spanning tree of the graph:
The following figure illustrates the image produced using Spanning Tree Method, when
applied to the example of the previous paragraph.

According to subset method, the set of images is divided into four subsets of neighboring images. At each subset the spanning tree procedure is followed and and a new image is produced. From these four new images the final image is produced following the same method. For mosaicing 4X4 images the evaluation of the error over twenty trees is required (four for each one of the four subsets of 2X2 images and four for the four intermediate images). In contrast, the spanning tree procedure acquires the evaluation of 100352 trees.
The following figure illustrates the image produced using subsets method, when applied
to the example of the previous paragraph.

According to the growing tree method, one spanning tree is build as follows: The nodes of the first row of the grid are connected. The nodes of the first column of the grid are connected. For the rest nodes the matching errors with their upper and their left neighbor are compared. The edge which corresponds to the smaller of the two errors is then selected. A spanning tree is build and then the position of the images can be determined and finally the image can be produced.
The following figure illustrates the image produced using Growing Tree Method, when
applied to the example of the previous paragraph.

Image registration methods can be utilized to match spatially two images which are
acquired from the same part of a painting. The following images correspond to the same
painting, which is acquired in the visible and x-ray regions of the spectrum (from left to
right, respectively):

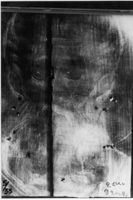
Since acquisition systems are not perfect, position misalignment may occur during the
acquisition of the x-ray image. Thus, a point in the visible image may not correspond to
the same point in the x-ray image. Detection of misalignment can be easily performed by
superposition of both images in one color image. Hue shifts in the resulting color image
indicate regions of strong misalignment. As an example, the color image that is formed by
the visible and x-ray images is displayed below:

In this example, misalignment is mainly exhibited in the area of the nose (indicated by
the red hues). Registration is a process that transforms one of the source images, in
order to match it spatially with the other one. The superposition of the visible and the
registered x-ray image is shown below:

One of the most common problems which deteriorates the quality of Byzantine icons is
the appearance of cracks on them. In order to confront this problem we detect the location
of cracks and apply various restoration filters.


Varnish oxidation is a phenomenon that can degrade seriously the overall visual appearance of old paintings. Dirt, smoke as well as other degradations deteriorate the situation even more. The end result is that colors faint and the painting appears brown or black. This is particularly true for icons or church murals, where candle smoke degrades icon colors. In many cases, this degradation can affect the artistic value of a painting. The process of removing this oxidation layer is performed by conservation experts. It is a time-consuming process which does not always promise guaranteed success. Indeed, the prevailing environmental conditions as well as the chemical properties, which are exhibited by the wide spectrum of different varnishes, make the task of selecting the appropriate cleaning process quite difficult.
In many cases, a trial and error approach is implemented, whereas in small regions ("samples") of the painting, chemical cleaning substances are applied in order to select the most appropriate one, that will be subsequently utilized to clean the entire painting. Digital image processing techniques can be applied for color restoration, aiming at obtaining an estimation of the original visual appearance of a painting, without extensive chemical cleaning treatment of its surface.
The following images depict an example of digital image processing restoration, of the
original color of a painting. The right part of a Byzantine painting was chemically
cleaned:

The left part of the painting, that was not cleaned, is shown below, along with the
digitally processed version. It is obvious that much of the original color information is
restored.


We have studied the reconstruction of the images mapped or painted on curved surfaces. When taking a picture of a scene mapped on a curved surface, the scene is distorted due to the projection of the geometry on the camera plane. If the curved surface is convex, it is not possible to obtain the entire scene on the surface, in only one image. In this study, we consider various images taken from different viewpoints, using monocular vision, in order to obtain the reconstruction of the complete scene by projection, flattening and mosaicing.


Left and right images of a church arch.
We explain how one can find a virtual image representation, where the intersection of the two axes is matched with the image center. In monocular vision, in order to backproject an image on the curved surface we need to find the localization parameters. These parameters consist of the three rotation angles, each corresponding to an axis of the 3D coordinate space. For each image taken from a different viewpoint we derive its localization based on a certain a priori knowledge. In this sense we assume known the equations of the projections for two parallels from the curved surface to the image.
We calculate the common normal of the two curves and afterwards we find the localization parameters. Based on the localization parameters we can flatten the respective description of the object. The result is an image containing a picture without geometrical distortions caused by the perspective view of the curved surface.


Left and right images of a church arch.
However, certain geometrical distortions are caused by the fact that different sized areas on the curved surface project to identical sized areas on the image. We derive the equation of the perspective distortions when projecting a scene that is mapped on a cylindrical surface. These regions which contain severe image distortions are not appropriate to be used for the representation of the scene. We evaluate the lower and the upper bounds of the number of views needed in order to represent the entire scene mapped on a cylinder when considering the distortions produced by perspective projection.
Image reconstruction is done through mosaicing. An automatic mosaicing method is proposed to be applied on the flattened images in order to obtain the complete scene.

The representation of the painting from the arch. The mosaiced scene can be visualized on a new synthetic surface by a mapping procedure. The proposed method is appropriate for the representation of mural paintings located on curved surfaces ( columns, vaults, etc. ).



Original images of a cup.



Flattened images.

Result of the mosaicing.

Virtual image of the cup after mosaicing.
![]()
![]()